Analogy of the divided line

Part of a series on
Plato
Early life · Works · Platonism
Epistemology · Idealism / Realism
Theory of Forms
Form of the Good
Third man argument
Euthyphro dilemma · Five regimes
Philosopher king
Allegories and metaphors
Ring of Gyges · The cave
The divided line · The sun
Ship of state · Myth of Er
The chariot
Related articles
The Academy in Athens
Socratic problem
Commentaries on Plato
Middle Platonism · Neoplatonism
Neoplatonism and Christianity

Plato, in his dialogue The Republic Book 6 (509D–513E), has Socrates explain through the literary device of a divided line his fundamental metaphysical ideas as four separate but logically connected models of the world. The four models are arranged into a first pair for the visible world, and a second pair for the purely intelligible world. The models are described in succession as corresponding to increasing levels of reality from common illusion, to belief, to reasoning, and then to philosophical understanding.

The analogy of the divided line immediately follows another Platonic metaphor, that of the sun, and is in turn followed by the Allegory of the Cave.

Contents

Imagine a line divided

In The Republic (509d-510a), Plato describes the Divided Line this way:

Now take a line which has been cut into two unequal parts, and divide each of them again in the same proportion, and suppose the two main divisions to answer, one to the visible and the other to the intelligible, and then compare the subdivisions in respect of their clearness and want of clearness, and you will find that the first section in the sphere of the visible consists of images. And by images I mean, in the first place, shadows, and in the second place, reflections in water and in solid, smooth and polished bodies and the like: Do you understand?

Yes, I understand.

Imagine, now, the other section, of which this is only the resemblance, to include the animals which we see, and everything that grows or is made.[2]

The visible world

Thus AB represents shadows and reflections of physical things, and BC the physical things themselves. These correspond to two kinds of knowledge, the illusion (εἰκασία eikasia) of our ordinarily, everyday experience, and belief (πίστις pistis) about discrete physical objects which cast their shadows.[3] In the Timaeus, the category of illusion includes all the "opinions of which the minds of ordinary people are full," while the natural sciences are included in the category of belief.[3]

The intelligible world

According to some translations,[4] the segment CE, representing the intelligible world, is divided into the same ratio as AC, giving the subdivisions CD and DE (it can be readily verified that CD must have the same length as BC[5]):

There are two subdivisions, in the lower of which the soul uses the figures given by the former division as images; the enquiry can only be hypothetical, and instead of going upwards to a principle descends to the other end; in the higher of the two, the soul passes out of hypotheses, and goes up to a principle which is above hypotheses, making no use of images as in the former case, but proceeding only in and through the ideas themselves (510b).[2]

Plato describes CD, the "lower" of these, as involving mathematical reasoning (διάνοια dianoia),[3] where abstract mathematical objects such as geometric lines are discussed. Such objects are outside the physical world (and are not to be confused with the drawings of those lines, which fall within the physical world BC). However, they are less important to Plato than the subjects of philosophical understanding (νόησις noesis), the "higher" of these two subdivisions (DE):

And when I speak of the other division of the intelligible, you will understand me to speak of that other sort of knowledge which reason herself attains by the power of dialectic, using the hypotheses not as first principles, but only as hypotheses — that is to say, as steps and points of departure into a world which is above hypotheses, in order that she may soar beyond them to the first principle of the whole (511b).[2]

Plato here is using the familiar relationship between ordinary objects and their shadows or reflections in order to illustrate the relationship between the physical world as a whole and the world of Ideas (Forms) as a whole. The former is made up of a series of passing reflections of the latter, which is eternal, more real and "true." Moreover, the knowledge that we have of the Ideas – when indeed we do have it – is of a higher order than knowledge of the mere physical world. In particular, knowledge of the forms leads to a knowledge of the Idea (Form) of the Good.[1]

The following table summarizes the analogy of the divided line:

Segment Type of knowledge Type of object
DE (highest) Philosophical understanding (noesis) Ideas (Forms), especially the Idea (Form) of the Good
CD Mathematical reasoning (dianoia), including theoretical science Abstract mathematical objects, such as numbers and lines
BC Beliefs about physical things (pistis), including empirical science Physical objects
AB (lowest) Opinions, illusions (eikasia) "Shadows" and "reflections" of physical objects

Metaphysical importance

The allegory of the Divided Line is the cornerstone of Plato's metaphysical framework. This structure, well hidden in the middle of the Republic, a complex, multi-layered dialogue, illustrates the grand picture of Plato's metaphysics, epistemology, and ethics, all in one. It is not enough for the philosopher to understand the Ideas (Forms), he must also understand the relation of Ideas to all four levels of the structure to be able to know anything at all. In the Republic, the philosopher must understand the Idea of Justice to live a just life or to organize and govern a just state.

The Divided Line also serves as our guide for most past and future metaphysics. The lowest level, which represents "the world of becoming and passing away" (Republic, 508d), is the metaphysical model for a Heraclitean philosophy of constant flux. The second level, the world of fixed physical objects, became Aristotle's model. The third level might be a Pythagorean level of mathematics. The fourth level is Plato's own reality, the world of highest level Ideas.

Epistemological meaning

Plato holds a very strict notion of knowledge. For example, he does not accept expertise about a subject (the Gorgias,482d), nor direct perception (the Theatetus), nor true belief about the physical world (the Meno) as knowledge. For knowledge, he also requires philosophical understanding of the relevant Ideas (Forms), as a basis for proper justification at all other levels of the Divided Line. Thus, for this reason, in most of the "early, Socratic" dialogues, Socrates denies knowledge both to himself and others.

For the first level, "the world of becoming and passing away," Plato expressly denies the possibility of knowledge.[6] Constant change never stays the same, therefore, properties of objects must refer to different Ideas at different times. Note that for knowledge to be possible, which Plato believed, the other three levels must be unchanging. The third and fourth level, mathematics and Ideas are already eternal and unchanging. However, to ensure that the second level objective, physical world is also unchanging, Plato, in the Republic, Book 4[7] introduces axiomatic restrictions that prohibit both motion and shifting perspectives.[8][9]

Notes

  1. ^ a b "divided line," The Cambridge Dictionary of Philosophy, 2nd edition, Cambridge University Press, 1999, ISBN 0521637228.
  2. ^ a b c Plato, The Republic, Book 6, translated by Benjamin Jowett, online
  3. ^ a b c Desmond Lee and Rachana Kamtekar, The Republic, Notes to Book 6, Penguin, 1987, ISBN 0140449140.
  4. ^ Older Greek texts do not differentiate unequal from equal (ανίσα, αν ίσα).
  5. ^ Let the length of AE be equal to 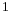\scriptstyle 1 and that of AC equal to 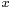\scriptstyle x, where 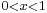\scriptstyle 0 < x < 1 (following Socrates, however, 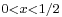\scriptstyle 0 < x < 1/2; insofar as the equality of the lengths of BC and CD is concerned, the latter restriction is of no significance). The length of CE is thus equal to 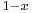\scriptstyle 1-x. It follows that the length of BC must be equal to 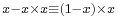\scriptstyle x - x \times x \equiv (1-x)\times x, which is seen to be equal to the length of CD.
  6. ^ Cratylus 439d
  7. ^ Republic 4.436b
  8. ^ Plato's Principle of Non-Contradiction (Republic, 4.436b) for the objective, physical world is presented with three axiomatic restrictions: The same thing ... cannot act or be acted upon ... in contrary ways ... (1) in the same part (2) in relation to the same thing (3) at the same time.
  9. ^ James Danaher, The Laws of Thought "The restrictions Plato places on the laws of thought (i.e., "in the same respect," and "at the same time,") are an attempt to isolate the object of thought by removing it from all other time but the present and all respects but one."

External links